Optimum Insulation Thickness Distribution for Heat Loss Uniformity from Heated Corrugated Pipes
Energy loss from fluids flowing across long distances presents a problem in many applications. In the oil and gas industry, for example, crude oil can change in viscosity when modest changes in temperature are realized. This can lead to added pumping power requirement and thus more heat input and/or heating stations along the way. The same problem could be faced in sewage and waste water transport, irrigation, and many other industries, when energy gain could be substituted for energy loss as the problem treated.
A number of industrial applications use pipes and ducts that are of nonuniform diameter—so-called corrugated pipes. Insulating such pipes results unequal heat loss along the axis of the pipe. This, in turn, may result in more heat loss than permissible or inefficient use of insulation material. In other cases, fouling and deposition can alter the shape of a uniform-diameter pipe, either internally or externally, or both.
The problem of optimally insulating a sinusoidally-corrugated pipe in order to minimize heat transfer is addressed here. Without loss of generality, we deal with heat loss from the pipe. The flow is assumed laminar and fully-developed. In a previous research effort, the author investigated the existence of a semi-analytical solution to the problem of optimal insulation of a corrugated pipe. The assumptions necessary to make the problem accessible analytically rule out most meaningful physics. Here, COMSOL Multiphysics® is used to find optimum insulation thickness of a sinusoidal pipe. The objective is to force uniform heat loss through the pipe surface, thus eliminating wasted insulation material. Three methods are used: simple ‘parametric study’ to the problem, the optimization module, and using COMSOL as an external objective function evaluation tool through LiveLink™ for MATLAB®.
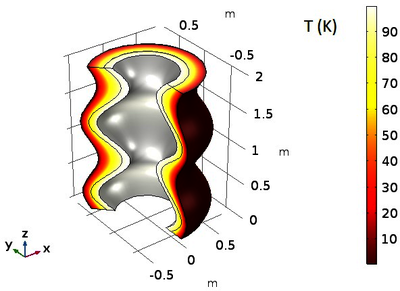
Initial results show that the first two methods converge to almost the same result, given that the complexity of the insulation layer is kept the same. Specifically, when the “parameter” is embedded within a sinusoidal pipe profile function, the phase of the insulation material geometry approximates the results given by the Nelder-Mead algorithm, for example. The second methods, however, can result in much better heat loss uniformity if the insulation function is taken to be a sixth-order polynomial. The coefficients of these polynomial are the decision variables to be optimized. It is found that heat transfer can almost be made uniform using such models and optimization algorithms. The figures below show a sample temperature distribution of one of the optimum cases and the associated heat fluxes across the three layers. Ongoing work (to be completed in time for the conference) includes modeling the internal and external flow and investigating how the added physics (fluid flow) affects influences the optimum insulation profile, as well as the effects of external natural convection.
Download
- bourisli_presentation.pdf - 1.77MB
- bourisli_poster.pdf - 0.66MB
- bourisli_paper.pdf - 0.79MB
- bourisli_abstract.pdf - 0.02MB
