Conducting Finite Element Convergence Studies Using COMSOL 4.0
We will show how to carry out convergence studies of the FEM error on a sequence of progressively finer meshes in COMSOL Multiphysics on the example of Lagrange elements of varying polynomial degrees, which will also bring out the benefit of using higher order elements.
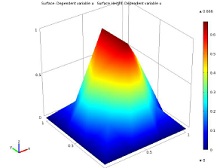
The sample studies will focus on Lagrange elements of degree 1 through 5. For these elements, the convergence order of the FEM error is computed. The expectation based upon the theory is that the convergence order is one degree higher than the polynomial degree of the Lagrange element used. We make use of the classical elliptic test problem provided by the Poisson equation with homogeneous Dirichlet boundary conditions on a square domain and a right-hand side function for which the PDE solution is known. In order to demonstrate the correctness and accuracy of the numerical solution, we will show how to estimate the convergence order of the FEM error and compare it with the theoretical estimates.
Download
- gobbert_presentation.pdf - 0.37MB
- gobbert_paper.pdf - 0.21MB
