
Today, we invite guest blogger Nagi Elabbasi of Veryst Engineering to share a modeling example of immersed beams.
When thin structures such as beams, plates, or shells are immersed in a fluid, their natural frequencies are reduced. The fluid also affects their mode shapes and is a source of damping. This phenomenon affects structures across a wide range of industries and sizes, from micro-scale structures (e.g. MEMS actuators) to larger structures (e.g. ships).
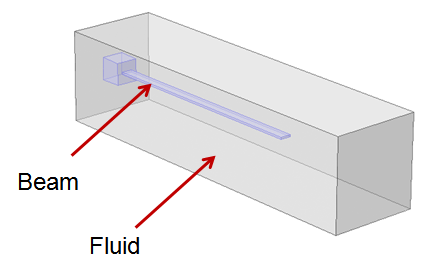
The Model: An Immersed Cantilever Beam
Today, we will take a look at a model of a cantilever beam immersed in a fluid:
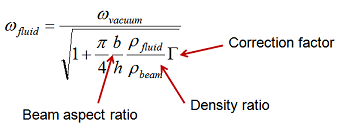
An approximate analytical solution of the form shown below is frequently used to estimate the natural frequencies of the immersed beam. This is estimated based on the structure-only natural frequencies, beam geometry, and the ratio of fluid-to-beam densities. The analytical expression approximately accounts for the added mass of the fluid that is displaced by the beam. It does not account for viscous effects.
A Multiphysics Approach to Determining Natural Frequencies and Mode Shapes
We at Veryst Engineering used COMSOL Multiphysics to determine the natural frequencies and mode shapes of an immersed cantilever beam. Then, we compared the results with the analytical approximation.
We set up the problem as a coupled acoustic-structure eigenvalue analysis. To account for the mass of the fluid, we selected a pressure acoustics formulation, and we accounted for damping due to fluid viscosity by including a viscous loss term. We assumed the fluid space to be sealed. The COMSOL software automatically detects the solid-fluid boundary and applies the necessary boundary conditions at the solid-fluid interface.
Solution
Below, you can see a table with the first and fourth natural frequencies (in kHz) of beams in vacuum, air, and water:
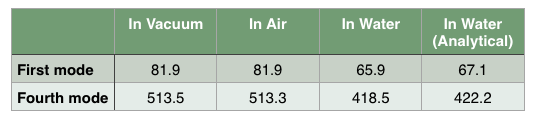
As expected, the results show that air has a minor effect on the beam, while water reduces the lowest natural frequencies of the beam by about 20%. Also shown in the table is the analytical estimate for a beam immersed in water. The analytical estimate is close to the COMSOL Multiphysics prediction for this relatively standard beam configuration.
Next, we can have a look at a couple of animations of our results.
The first animation depicts the fourth mode of deformation for a beam immersed in water:
Fourth mode shape of cantilever beam immersed in water.
The second animation demonstrates fluid pressure contours and fluid velocity arrow plots at a section along the beam, again for the fourth natural frequency of the beam.
Velocity and pressure contours for fourth beam natural frequency.
This modeling example involved a simple cantilever to illustrate the concept. However, the coupled structural-acoustic modeling approach used is also applicable to more realistic geometries, such as ship hulls and MEMS actuators.
About the Guest Author
Nagi Elabbasi, PhD, is a Managing Engineer at Veryst Engineering LLC. Nagi’s primary area of expertise is modeling and simulation of multiphysics systems. He has extensive experience in finite element modeling of structural, CFD, heat transfer, and coupled systems, including fluid-structure interaction, conjugate heat transfer, and structural-acoustic coupling. Veryst Engineering provides services in product development, material testing and modeling, and failure analysis, and is a member of the COMSOL Certified Consultant program.




Comments (45)
Aimaiti Rehemanjiang
May 9, 2014I am very interesting about this simulation. this is very cool simulation. Can you tell some information about the Young’s modulus, Poisson’s ratio for air ?? because in order to add air as environment in Structural Mechanics interface, I have encountered this problem … thank you !!!
Aimaiti Rehemanjiang
May 9, 2014I think , when you consider the Air case in your simulation. You might use those information of air I think …
Nagi Elabbasi
May 9, 2014Hi Aimaiti, I am glad you liked the simulation!
You should not use the structural module only for this. You need instead acoustic-structural interaction with the air/fluid modeled as an acoustic medium. In that case the required material parameters for the fluid are the density and the speed of sound. Since we accounted for viscous dissipation then you also need the dynamic viscosity of the fluid.
I believe this simulation without the viscous damping only requires the basic COMSOL Multiphysics package. You need the Acoustics Module if you want to include viscous damping, thermo-acoustic effects or other features like linearized Euler flow.
Danilo D'Agostino
July 4, 2014Hi Nagi,
It is a very interesting example, but I am wondering which boundary conditions have to be setted besides the fixed constraint at L=0?
Jin Lee
July 29, 2014Dear Dr. Elabbasi,
I am just wondering how you’ve calculated the correction factor for the analytical solution above. Thanks!
Dr. Lee
Nagi Elabbasi
August 11, 2014Hi Danilo,
The boundary conditions are quite simple. The beam is fixed at one end as you noted, COMSOL takes care of the acoustic-structure boundary, and you specify an appropriate acoustic boundary conditions on the faces of the fluid region. In this example it was a hard sound boundary since it is a sealed space.
Nagi Elabbasi
August 11, 2014Dear Dr. Lee,
We used this reference to calculate the correction factors: CA Van Eysden, JE Sader, Resonant Frequencies of a Rectangular Cantilever Beam Immersed in a Fluid, Journal of Applied Physics, 100 (2006)
Yuanyu Yu
August 19, 2014Dear Dr. nagi,
I created a circular plate with air above it using acoustic-structural interaction physics. The circular plate is clamped as the boundary condition. By using the eigenfrequency study, but the result is wrong (with imaginary part, and the value of real part is very small)… I set Linear Elastic Material to the plate.
What is wrong? Thanks!
Nagi Elabbasi
August 20, 2014Dear Yuanyu,
What you did seems right. Try plotting the mode shapes at these reported frequencies and maybe you will spot a wrong boundary condition or material setting. Also try tightening the eigensolver convergence tolerance, and increasing the maximum number of eigenvalue iterations.
Anulekha Majumdar
September 18, 2014Dear Dr. Nagi
I read your article and I am doing something similar to your work. Since I am new to this software, can you please suggest me how to add damping in the material when doing the eigenfrequency analysis in water. I tried directly adding damping from linear elastic material, but the result is not near the experimental values. Also that during underwater analysis, do we have to add PML (perfectly matched layer) always?
Thanks in advance
Anulekha Majumdar
Jean Cacheux
June 18, 2015Hi,
I am trying to use this model with COMSOL 4.3. Do you know if it is possible ? Cause I can’t see any frequency shift when putting the cantilever in liquid. Plus I would expect a loss in the deformation amplitude, which I can’t observe neither. Could you share the file you’re using for the simulation ?
Thank you,
Jean
Nagi Elabbasi
June 21, 2015Hi Jean,
I see no reason for this not to work with COMSOL 4.3. If you don’t get a frequency shift try artificially increasing the fluid density to see if the lack of shift is physical or a modeling error. Also you will not necessarily get a reduction in deformation amplitude in an eigenfrequency analysis since the mode shapes are normalized. If you do a harmonic frequency analysis then you see a vibration amplitude reduction.
Regards,
Nagi
Waqas Waheed
June 24, 2015Hi,
Can you please mention the dimensions of the cantilever? Did you also calculate its Q-factor?
Thanks
Waqas
Ryan Tancin
June 30, 2015Hi,
My version of COMSOL 4.4 only has the Pressure Acoustics module, not the acoustic structure interaction, is it still possible to do this simulation with that module? Thanks in advance.
Ryan
Nagi Elabbasi
June 30, 2015Hi Ryan,
You probably only see Pressure Acoustics because you don’t have the Acoustics Module. See the Product Specification webpage for more details: http://www.comsol.com/products/specifications/acoustics/
Regards,
Nagi
Marco Tr
August 19, 2015Hi,
I am trying to define the mechanical damping in my analysis with comsol 4.4. I followed a tutorial where it is recommended to follow these steps:
1 -On the Physics toolbar, click Attributes and choose Mechanical Damping.
2 -In the Settings window for Mechanical Damping, locate the Damping Settings
section.
3 -From the Damping type list, choose Isotropic loss factor.
4- From the ηs list, choose User defined. In the associated text field, type 0.001.
But I cannot find either Attributes or Mechanical damping on my software.
Could anyone help to tackle that issue?
May thanks
Nagi Elabbasi
August 19, 2015Hi Marco, that may be because you don’t have the right module. You need the Structural Mechanics module to include material damping. See the Product Specification page for more details: http://www.comsol.com/products/specifications/structural-mechanics/. Regards, Nagi
Levin Dieterle
January 18, 2016Hi,
I’m very interested in this model. Would it be possible to make the COMSOL file available, to see how the interfaces are set. Thanks.
Regards,
Levin
Nagi Elabbasi
January 18, 2016Hi Levin, orry I cannot share the model file but if you have specific questions I will try to answer them. Regards, Nagi
murat gel
February 17, 2016Hi, Is the model available for download?
Nagi Elabbasi
February 17, 2016Hi Murat, sorry I cannot share the model but I suggest you check out COMSOL Application ID 14731 titled Vibrating Micromirror with Viscous and Thermal Damping. It highlights many of the features used in this immersed beam model. Regards, Nagi
Javier Rivero
May 6, 2016Hi Nagi Elabbasi,
I’m interested in the solution of eigenvalue problems involving fluid flows and when I try to solve a very simple case, I don’t make it work. Eigenvalues are all NaN. I’m pretty sure it is because in the eigenvalue problem COMSOL doesn’t perturbe the local inertia term and this term is the only one appearing in the mass matrix. Does your computation takes into account this term?? Even if you don’t I should give some results because you have time derivative anywhere else, but in my case I’m interested in hydrodynamical modes. Regards, Javier.
Nagi Elabbasi
May 6, 2016Hi Javier, I can’t think of a good reason why you’re getting NaN eigenvalues. The mass matrix is getting a contribution from the beam itself, which comes from the solid mechanics model. It also gets contribution from the fluid which is straightforward for COMSOL to calculate and does not need a perturbation analysis. Regards, Nagi
Deepak Singh
July 20, 2016Sir,
I want to calculate the natural frequency of a plate which is coupled with water only on one side,
so should I try fluid-structure interaction or acoustic-structure interaction?
Satthiyaraju M
January 9, 2017Dear Nagi, I have solved only using solid mechanics_eigen frequency study. Defined BC’s are cantilever beam with surrounding medium water. I have created block around the cantilever beam and applied water properties and fixed all sides of the outer block. I got values of eig freqs. But I don’t know whether it’s correct or not? I could not get the proper mode shapes…. Please rely how to model the same. thank you very much.
Nagi Elabbasi
January 9, 2017Dear Satthiyaraju,
One way to check if your model set up is correct is to either use a stiff beam material or a low density fluid material (air) for validation. The results should be very similar to the structural-only analysis in this case, both in terms of frequencies and mode shapes. After that you can go back to the properties material/fluid properties and compare against analytical frequency estimates if possible, like the one I used above. Note also that there may be additional acoustic-dominant modes that you have to ignore when looking at the beam modes shapes.
Vinit Kumar
January 14, 2017Dear Nagi,
It is an interesting simulation. I was trying it, but, I was wondering the eigenfrequencies returned by Comsol were complex. I am curious to know how we can interpret complex eigenfrequencies.
Thanks!
Nagi Elabbasi
January 19, 2017Dear Vinit,
If the eigenfrequencies are complex that’s due to damping. The ratio of the imaginary to real part of the eigenfrequency is roughly equal to the damping ratio (if the imaginary part is small compared to the real part). In this model you can add damping to the structure or the fluid, or both. Fluid damping requires a more accurate fluid formulation as explained in the discussion above.
Deepak Singh
January 20, 2017Sir,
I want to calculate the natural frequency of a plate which is coupled with water only on one side,
how to find?
Hemanta Dikshit
December 10, 2021Did you get the natural frequency when water only on one side of plate?
Rahul Goyal
February 10, 2017Respected Sir,
I need to connect dependence of natural frequency on viscosity of fluids, kindly tell me how to do it in comsol.
Nagi Elabbasi
February 10, 2017Dear Deepak, I guess you have water on one side and air on the other side of the plate. In that case, you can develop a similar model to the one I described with acoustics on one side only and ignore the air.
Nagi Elabbasi
February 10, 2017Dear Rahul, if you want to find the dependence of the natural frequency on viscosity I suggest you do a parametric sweep over the viscosity, for the eigenfrequency solver. If you meant that the viscosity is a function of frequency then you can set it be a function of frequency instead of a constant value.
Rahul Goyal
February 10, 2017Sir,
Thanks for the reply. Yes I want to see that how natural frequency of beam changes with the change of fluid properties i.e. viscosity. I did that but graph is coming constant Frequency vs Viscosity, I think that comsol is not taking into account the viscosity. Can you please tell me hoe to do it?
Rahul Goyal
March 1, 2017Sir, can you tell me how did you include the viscous loss term for considering viscous damping.
Nagi Elabbasi
March 4, 2017Dear Rahul,
To include the effect of viscosity in the pressure acoustics formulation (as in the blog example above) you should select Fluid Model=Viscous in the Pressure Acoustics Model settings. This option is only available if you have the Acoustics Module.
Keep in mind that this is an approximate way to account for the effect of viscosity. Check out the Thermoviscous Acoustics COMSOL formulation for a more accurate, but more computationally demanding, way to account for viscous effects. See also COMSOL Application Gallery ID 14731 titled “Vibrating Micromirror with Viscous and Thermal Damping” for an example.
Regards,
Nagi
Mehul Patel
January 3, 2018Hello Sir,
Is it feasible to use piezoelectric effect multiphysics by using solid mechanics, electrostatics, and pressure acoustic for analysis in underwater environment of cantilever beam?
As I want electric potential in fluid or water.
Fateme Aghighi
February 22, 2018Hello,
I am trying to create a similar model in Comsol 5.2a. I am not sure how to set up a coupled acoustic-structure eigenvalue analysis. I have Acoustic-Structure Interaction, Frequency Domain and created the eigenfrequency study. But it seems like as I change the size of the fluid the natural frequencies changes! Where should we define the fact that water is just the ambient fluid? I also used PML but it didn’t make a difference.
Thanks,
Fateme
Nagi Elabbasi
February 26, 2018Dear Hyo Geon,
What I meant is that the standard pressure acoustics available in the base COMSOL package does not have the capability to account for viscous damping. There are multiple formulations that can account for that damping, all of them in the Acoustics module. Note also that for the specific geometry I used in this problem the viscous damping is insignificant; the main focus was the added mass of the fluid. For a COMSOL example where the viscous damping is important, check out Application Gallery model #14731 titled “Vibrating Micromirror with Viscous and Thermal Damping”.
Nagi Elabbasi
February 26, 2018Dear Mehul, I believe what you want to do is feasible in COMSOL.
Nagi Elabbasi
February 26, 2018Dear Fateme,
COMSOL will report structural dominated natural frequencies that should not be affected by the size of the fluid domain, as long as the fluid domain is not too small. These are the frequencies of interest to us in this problem. COMSOL also reports acoustic dominated natural frequencies that are strongly affected by the shape and size of the acoustic domain. Plotting the mode shape is one easy way to find out the “type” of each frequency.
Sanford Siegel
May 26, 2018This article is nice and everything, but do you think you could actually tell us how to do it??????????
Nebyat Weldearegay
November 7, 2018the paper is nice as a general information but there is no enough information on how to model it…..?
Darshan Soni
December 15, 2019Can you tell me how you converted the complex eigenfrequency values to a real natural frequency, your animation has complex eigenvalue but you have written a real value in the result table.
Sameer Bhakare
February 13, 2024I wants to do frequency analysis of link submerged in water. how can I do that, plz explain