
Nowadays, the need for travel is growing — and with it, transportation alternatives that are greener; less noisy; and, of course, faster. But what moves must eventually stop, and while most planes, trains, and automobiles use mechanical braking, this type of braking can cause damage and become unsafe at high speeds. Not so with eddy current braking. Here, we investigate the potential for this type of frictionless braking and the phenomenon behind this effect.
Slowing Down Safely with Eddy Current Brakes
If Train A leaves Boston toward New York City at 8 a.m. traveling 35 miles per hour (mph), and Train B leaves New York City toward Boston at 8:30 a.m. traveling 50 mph, at what time do the two trains meet, assuming the cities are roughly 200 miles apart?
A typical school math problem involving two trains and distance, rate, and time is so classic that it has become a TV trope. But textbook authors (and television writers) may need to update some details as new developments in transportation technology emerge. For instance, high-speed commercial trains often travel at an average speed of 180 mph, shaving a lot of time off the journey. So, future train math problems may need to factor in much higher speeds and use two cities that are farther apart.

The Shanghai magnetic levitation train, the fastest commercial high-speed electric train in the world. Image by Andreas Krebs — Own work. Licensed under CC BY-SA 2.0, via Flickr Creative Commons.
We couldn’t practically consider these questions without looking into frictionless braking technologies. If a traditional train would travel at 180 mph using mechanical brakes, the brakes might not stop it in time — or at all. The faster a train moves, the harder the friction brakes have to work to dissipate the kinetic energy, which means the brakes run a greater risk of wearing out altogether. To combat this, many trains use dynamic braking that reduces wear and tear, but the friction-based components can still fail.
When the vehicle has the means, regenerative braking is preferred. For this type of frictionless braking, a (linear) motor or generator converts kinetic energy back into electric energy, which, at a later stage, can be reused for acceleration. Less energy efficient (but still better than mechanical braking) is the use of eddy current braking. With eddy current braking, all generated electric energy is converted directly into heat. Since the energy conversion takes place without mechanical contact, these systems tend to be much more robust than friction-based systems. Another advantage is that these systems will still work, even if there isn’t any mechanical contact between the vehicle and the track in the first place. This is the case for magnetically levitating (maglev) vehicles, such as the Shanghai maglev and a Japan Railway train that set a record-breaking top speed of 374 mph.
Eddy Current Braking Systems in the Real World
So, how do braking systems using eddy currents work in the real world? One design developed and tested by a German railway company uses a linear array of eight electromagnets fitted between the wheels, at a distance of about 7 mm from the rail. Train operators can turn on these magnets when they want to slow down, which causes the magnets to generate a magnetic field that expands into the rail. Because the rail is stationary, it will experience a concentrated magnetic field moving in at high velocity, and strong eddy currents will develop. These eddy currents are a result of the rail resisting the enforced change in magnetic flux: They flow in such a direction that the rail generates its own magnetic field, which tries to counteract (expel) the applied one. The two magnetic fields repel each other and a braking force results — meaning the train will come to a frictionless stop.
Advantages of this type of frictionless braking include being finely controlled, relatively inexpensive, and free of pollution and noise. The downside to using this type of braking is that the electromagnetic parts can occasionally interfere with train signaling equipment. Another limitation is that a finite velocity is required (it will not work as a parking brake, for instance). And if there are a lot of trains braking quickly in a row in the same spot, the heat dissipated in the rails could expand them, leading to structural problems. Overall, though, eddy current brakes have a lot to offer high-speed transportation systems. Below, you can see examples of both a linear and rotary brake used in high-speed trains.


Linear eddy current brake in a German high-speed train (left). Image by Sebastian Terfloth — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons. Closeup of an eddy current brake used on a high-speed Japanese train (right). Image by Take-y — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
Linear Versus Circular Eddy Current Brakes
There are two commonly used types of eddy current brakes: linear and circular. Linear brakes are the kind you find on a track for a train or rollercoaster, where the track works as part of the braking system. In a rollercoaster, the magnets are placed at the end of the track and metal strips are mounted on the side of the cars. Once the cars reach the magnets, the brakes start working because the magnets induce eddy currents in the metal. As an extra safety precaution, rollercoasters typically use permanent magnets so that the brakes still work in case of a power outage.

Eddy current brakes on a rollercoaster track. Image by Stefan Scheer — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
Circular brakes also have one component that stays still while the other moves. In one version, the magnet is stationary while a metal disc rotates, and in the other design, the electromagnets move — coils are placed on a wheel that spins around a fixed shaft. Among other use cases, circular eddy current brakes come in handy when operating industrial machinery, especially for emergency shut off. If you want to stop a factory machine or a power tool like a circular saw, you could switch on the electromagnets to produce eddy currents and bring the metal wheel mechanism swiftly to a halt.
Let’s take a closer look at the physics behind eddy currents as well as two simulation examples that cover both linear and circular braking.
What Are Eddy Currents?
Eddy currents are loops of electrical current induced in conductors by a varying magnetic field. The currents are a result of Faraday’s law of induction.
The History of Eddy Currents
Eddy currents were first observed by 19th-century French Prime Minister François Arago. They are named for their resemblance to the swirling eddies in river currents, but eddy current swirls are typically observed in a metal sheet or disc. Scientist Michael Faraday was able to further explain Arago’s observations and formulated Faraday’s law of induction. Soon afterward, Emil Lenz postulated Lenz’s law.

Heinrich Friedrich Emil Lenz. Image in the public domain in the United States, via Wikimedia Commons.
Following Faraday’s law of induction, which focuses on the electromotive force that pushes the eddy currents into motion, Lenz’s law indicates the direction of the currents. Lenz realized that an induced current will always flow in such a direction that the current opposes the change that induced it. This means that eddy currents tend to cause a loss of energy (or, as is the case for braking systems, a conversion of kinetic energy into heat). Although eddy current losses are undesired for many applications, for uses like braking, they are perfect.
In 1855, French physicist Léon Foucault made a discovery about eddy currents that relates specifically to braking: In order to rotate a copper disc, the force required increases when the disc rotates with its rim between the poles of a magnet. While this is happening, the eddy currents induced in the metal heat the rotating disc.
In 1879, David E. Hughes demonstrated one of the first uses of eddy currents: metallurgical sorting. Since then, eddy currents have been used to identify and sort coins in vending machines and help metal detectors sense metallic objects.
Eddy Current Simulation in COMSOL Multiphysics®: Linear and Rotary Brake Designs
Modeling a Linear Brake with a Lenz’s Law Apparatus
You may recall a classroom physics experiment that uses eddy currents to demonstrate two laws of electromagnetism:
- Faraday’s law of induction
- Lenz’s law
If you don’t remember or have never seen this experiment, don’t worry: We’ll demonstrate it shortly. First, let’s take a look at eddy currents so we understand how the experiment works. We can see eddy currents in action with a Lenz’s law apparatus model, which includes a cylindrical magnet falling through a metal tube (in this case, copper).

Schematic (left) and photo (right) of a Lenz’s law apparatus.
As we talked about in the linear track examples, eddy currents are similarly generated inside the tube walls, and the opposing magnetic fields create a braking force that slows the motion of the magnet. As the velocity of the magnet increases, so does the opposing force. This means that at some point, the magnet will reach a terminal velocity where the magnetic braking force equals the force of gravity.
You can see these effects for yourself by using a Lenz’s law apparatus to figure out the falling magnet’s velocity and acceleration as it reaches its terminal velocity.
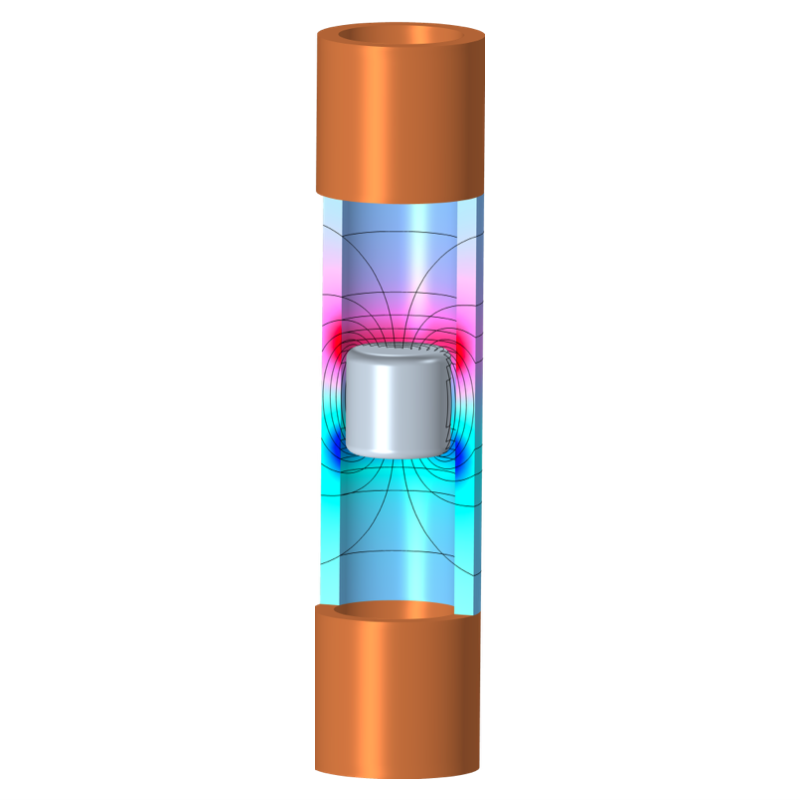
A 3D simulation of a magnet falling through a copper tube.
Modeling a Rotary Brake
Now that we’ve seen how eddy currents work in a linear brake, let’s look at how they work in a rotary brake. This model consists of a rotating disc and a permanent magnet. As Foucault discovered, the disc’s conductive properties produce eddy currents as it rotates within the permanent magnet’s magnetic field. Then, due to the forces from these currents, the disc slows down.
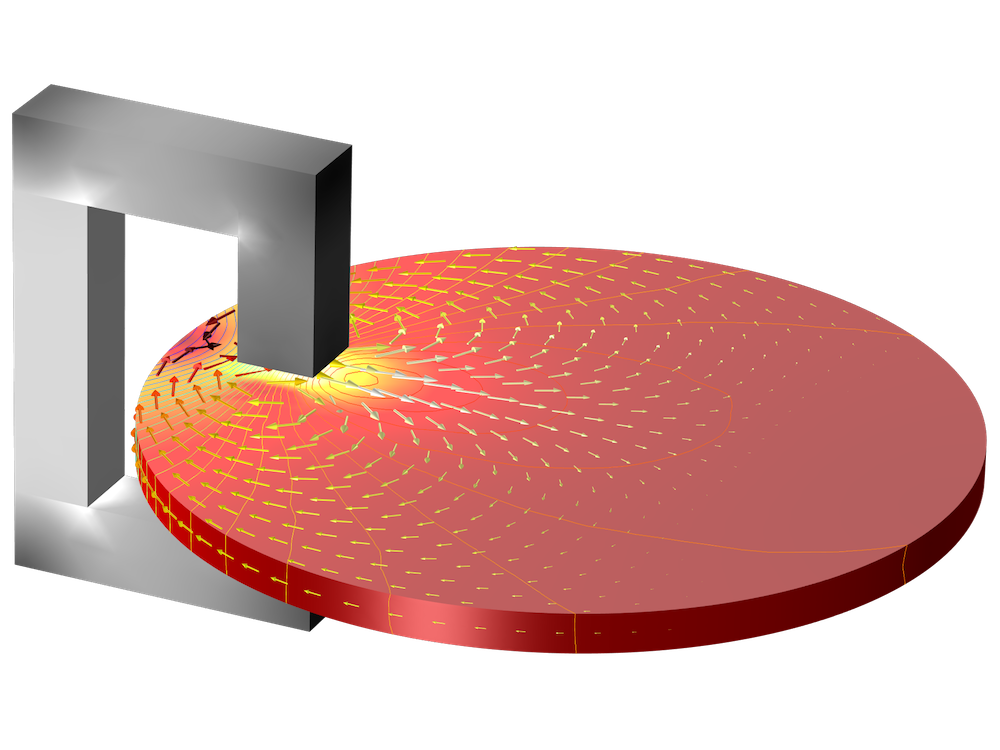
3D simulation of an eddy current brake.
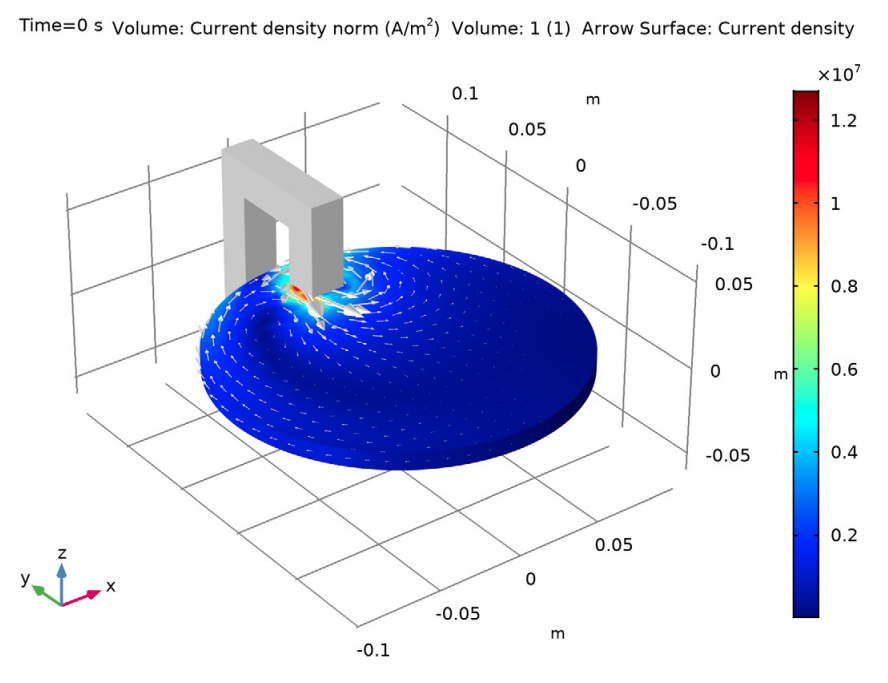
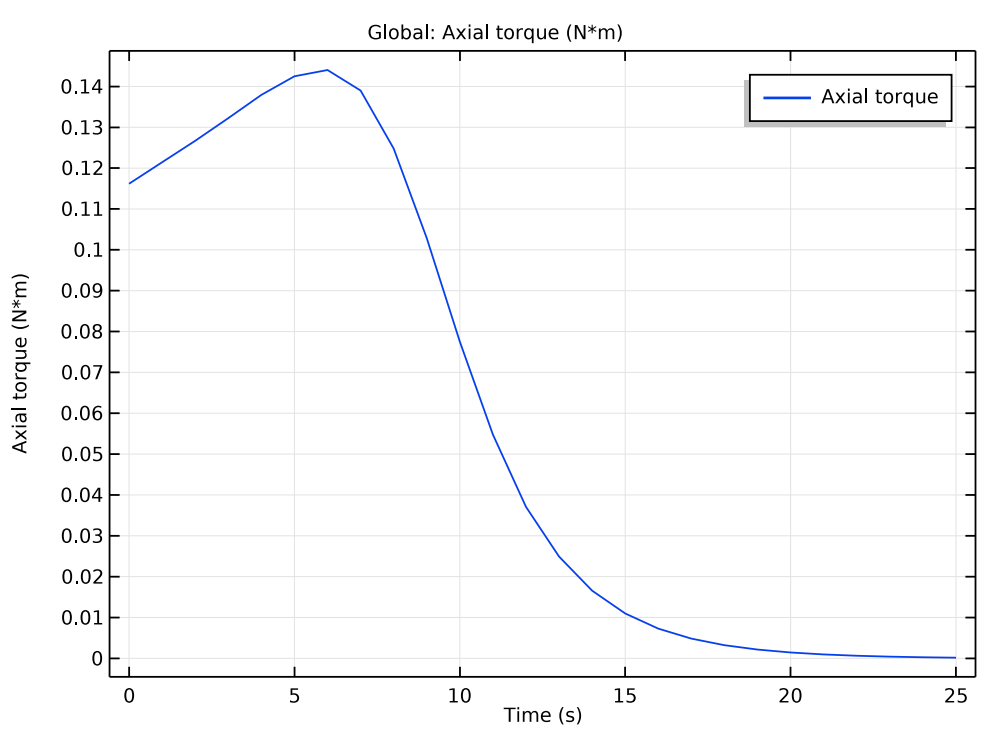
The total time it takes to bring your system to a halt (whether it is a car, train, or rollercoaster) depends on the strength of the magnets (the forces they exert on the disc) and the disc’s ability to dissipate the energy. In order to investigate this process, you can simulate eddy current brakes with tools that help you couple a dynamic equation (defining the rotation of the disc) with the finite element method (defining the torque). For example, in the images below, you can see the current density on the surface of the disc at t = 0 when the disc is still spinning (left) as well as the time evolution for the different braking factors.
3D model showing induced eddy current magnitude and direction at t = 0 s (left). Time evolution of the torque in the eddy current braking system (right).
Using electromagnetics modeling software, you can study the induced eddy current density and time evolution of the angular velocity, braking torque, and dissipated power.
Other Use Cases for Eddy Current Brake Designs
While eddy current braking systems are not yet in widespread use, their low cost and reliability makes them useful for:
- Elevators
- Industrial drilling rigs
- Amusement park rides like rollercoasters and drop towers
- Resistance in exercise machines
As regenerative braking is typically preferred in systems equipped with a large linear or rotary electric motor (such as those in maglev trains and electric cars), eddy current braking offers reliable replacement options for mechanical brakes or as emergency systems.
If you’d like to try your hand at improving eddy current braking for smoother, faster designs, or simply wish to investigate the eddy current braking phenomenon by calculating a magnet’s velocity and acceleration in a Lenz’s law apparatus, you can use the COMSOL® software. Perhaps you’ll come up with a new train math problem that’s better suited for the 21st century.
Next Steps
Learn more about how electromagnetics modeling software can help you understand, predict, and optimize the performance of static and low-frequency systems:
- Download the tutorial models featured in this blog post:
- Learn about electromagnetic waves theory





Comments (1)
Ranzi Umberto
March 11, 2019Thank-you. Very clear and step by step description is useful